jacobian 二維座標轉換積分

前言

vector a x b : vector a sweeps in direction of vector b creates the area
0=(ai+bj)x(ai+bj)=ab (i x j + j x i) => i x j = - j x i
vector(a,b) moved as vector (c,d) painted green area
green area=blue-yellow=orange-pink=ad-bc

類 jacobian 二維座標轉換積分

for U(x,y), V(x,y)
dU = Ux dx + Uy dy
dV = Vx dx + Vy dy

Assume:
U(x,y)=U, V(x,y)=V cross at (x0,y0)
U(x,y)=U+dU, V(x,y)=V cross at (x0+dx1,y0+dy1)
U(x,y)=U, V(x,y)=V+dV cross at (x0+dx2,y0+dy2)

Ux dx1 + Uy dy1= dU
Vx dx1 + Vy dy1= 0
Ux dx2 + Uy dy2= 0
Vx dx2 + Vy dy2= dV

let S= UxVy - VxUy
(dx1,dy1)= (Vy/S dU , -Vx/S dU)
(dx2,dy2)= (Uy/S dV ,  Ux/S dV)

Area(面積) = ad - bc = (dx1 dy2) - (dy1 dx2)
= (Vy/S dU) x (Ux/S dV) - (-Vx/S dU) x (Uy/S dV) = (UxVy - VxUy)/S^2 dU dV = 1/S dU dV

for S= UxVy - VxUy , 1/S is jacobian directly (直接就是jacobian)

Conclusion:

When U moves dU, and V moves dV, the area in U-V plane is dU dV
which projected to area of 1/(UxVy - VxUy) dU dV in X-Y plane

座標轉換(一次聯立方程求解)與行列式(面積,體積) Cramer's rule

2D 面積比求新座標 (二元一次聯立方程求解)

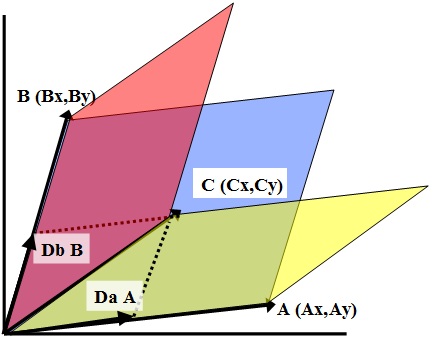
以原座標體系向量A(Ax,Ay),B(Bx,By)做為新座標體系單位向量
預將原座標體系之向量C(Cx,Cy)轉換成新座標(Da,Db)
(Cx,Cy)= C = DaA + DbB = (DaAx + DbBx , DaAy + DbBy)
AxDa + BxDb = Cx
AyDa + ByDb = Cy
座標轉換等於求取上面二元一次聯立方程Da,Db解

由圖中可見
C沿著平行於B的方向交A之處即為A上分量DaA
C沿著平行於A的方向交B之處即為B上分量DbB
A和C圍成黃色平行四邊形,與同高之A與DbB圍成平行四邊形相等面積
而A和B圍成藍色平行四邊形
預知Db=DbB/B可由 (A x DbB)/(A x B) =(A x C)/(A x B)=黃色面積/藍色面積
而面積可表為二向量放入形成之行列式
Db=(A x C)/(A x B)=Δb/Δ
|Ax Cx|    |Ax Bx|
|Ay Cy| /  |Ay By|
同理Da=紅色面積/藍色面積= (C x B)/(A x B)=Δa/Δ
|Cx Bx|    |Ax Bx|
|Cy By| /  |Ay By|
基本上
分母則為所有新座標軸形成之行列式
分子就是以待轉換向量代位分母行列式中欲求參數所屬之新座標軸向量

3D體積比求新座標 (三元一次聯立方程求解)

以原座標體系向量A(Ax,Ay,Az),B(Bx,By,Bz),C(Cx,Cy,Cz)做為新座標體系單位向量
預將原座標體系之向量D(Dx,Dy,Dz)轉換成新座標(Ea,Eb,Ec)
AxEa + BxEb + CxEc = Dx
AyEa + ByEb + CyEc = Dy
AzEa + BzEb + CzEc = Dz
座標轉換等於求取上面三元一次聯立方程Ea,Eb,Ec解

由圖中可見
D沿著平行於AB平面的方向交C之處即為C上分量EcC
AB平面和D圍成紅色平行體,與同高之AB平面與EcC圍成平行體相等體積
預知Ec=EcAB/CAB可由 (A x B x EcC)/(AxBxC) =(AxBxD)/(AxBxC)=紅色體積/藍色體積
而體積可表為三向量放入形成之行列式
Ec=(AxBxD)/(AxBxC)=Δc/Δ
|Ax Bx Dx|    |Ax Bx Cx|
|Ay By Dy| /  |Ay By Cy|
|Az Bz Dz|    |Az Bz Cz|
同理可得Ea,Eb